Floyd 和 Brent 判圈算法

发表于 2023-02-26 更新于 2024-05-02 分类于学知识 Waline：阅读次数：

今天刷 141. Linked List Cycle和 142. Linked List Cycle II学到了两个新的判断链表是否存在环的算法 - Floyd龟兔赛跑算法和 Brent判圈算法。

Floyd 龟兔赛跑算法

这个算法的核心思想是，如果有限状态机、迭代函数或者链表上存在环，那么在某个环上以不同速度前进的两个指针必定在某个时间会相遇。也就是说，对于一个链表，可以分别使用两个指针进行遍历，慢指针一次走一步，快指针一次走两步，如果快慢指针相遇了，那么说明链表中存在环。

当发现有环之后，让快指针停止，慢指针从当前位置继续向前遍历，并计算走过的步数。在慢指针与快指针再次相遇之后，慢指针走过的步数，就是环的长度。

如果要计算环的入口，那么可以将一个指针移动到链表的起点，另一个指针不动，然后使两个指针每次同时向前走一步，当二者再次相遇的时候，指针所在的位置就是环的起点。至于这个操作的原理，原谅我数学很差，想不明白，所以借浅谈判圈算法 - xyZGHio一文中的解释：

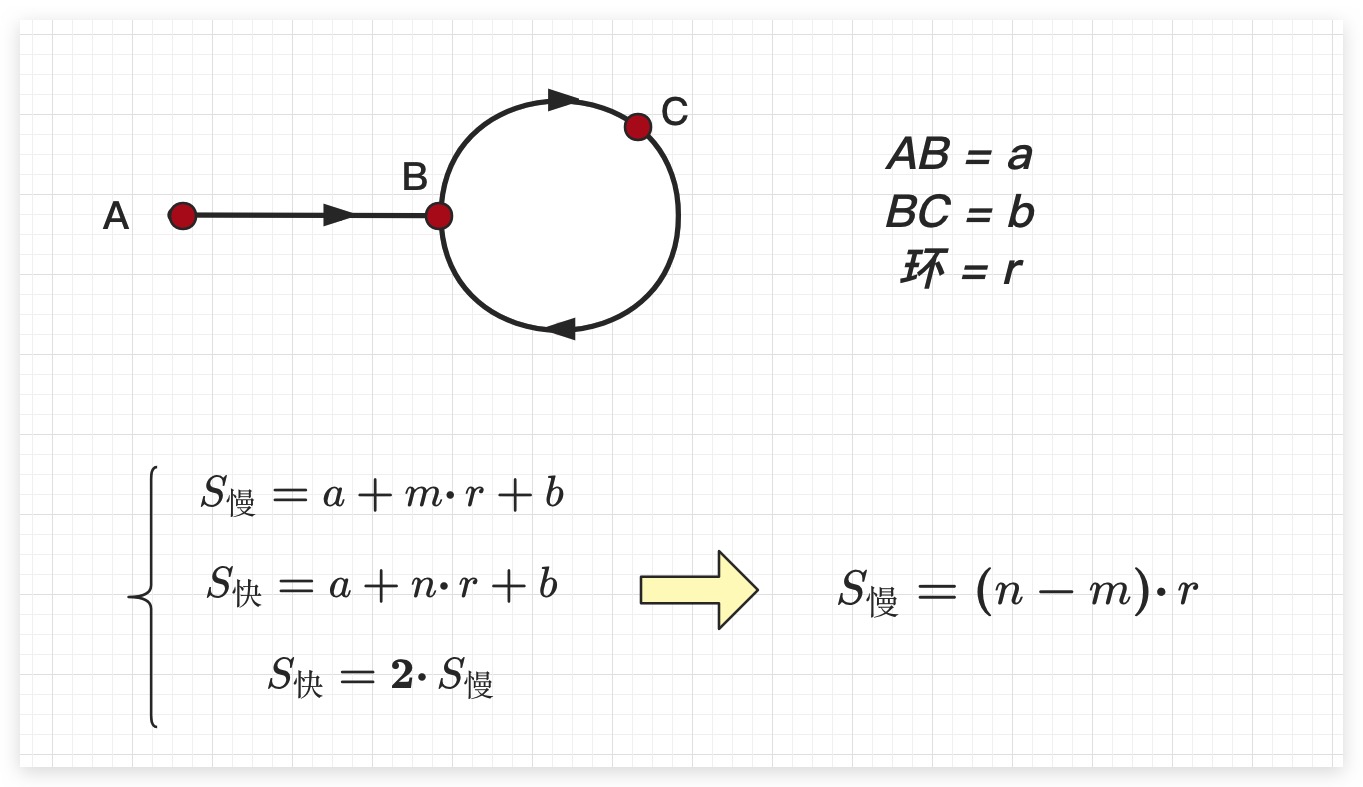
这里令起始处为 A、环的入口处为 B，在判断是否有环阶段时快慢相遇之处为 C。并记 AB 长度为 a、记 BC 长度为 b、环的长度为 r。且在判断是否有环过程中，快指针每次走 2 步、慢指针每次走 1 步。则快、慢指针相遇时，快指针走过的长度是慢指针走过长度的 2 倍。

此时不难看出，当快、慢指针相遇时，快、慢指针走过的长度均是环长度的整数倍。故如果期望找到环的入口位置，即 B 处。则只需在两个指针相遇之时，将其中任意一个指针放置到起始处 A，而另一个指针依然位于相遇处 C。然后两个指针按照每次均走 1 步的速度向前走，当二者再次相遇之时，即是 B 处。
原因在于，对于相遇后继续往前走的指针而言，由于其已经走过了若干圈环的长度，此时只需再走 a 步即可到达环的入口。这个地方换个角度想会更容易理解，如果该指针先走 a 步再走若干圈环的长度，其必然位于环的入口处；而对于相遇后从起始处 A 开始走的指针而言，其显然走 a 步后，必然也会位于环的入口处。故此时两个指针第二次相遇之时，说明他们均已经走完 a 步。即到达环的入口处。

代码：

/**
 * https://leetcode.com/problems/linked-list-cycle-ii
 */
public class Solution {
    /**
     * 找环的入口
     */
    public ListNode detectCycle(ListNode head) {
        if (head == null) {
            return null;
        }

        ListNode intersect = getIntersect(head);
        if (intersect == null) {
            return null;
        }

        ListNode ptr1 = head;
        ListNode ptr2 = intersect;
        while (ptr1 != ptr2) {
            ptr1 = ptr1.next;
            ptr2 = ptr2.next;
        }

        return ptr1;
    }

    /**
     * 找快慢两个指针交会的位置
     */
    private ListNode getIntersect(ListNode head) {
        ListNode slow = head;
        ListNode fast = head;

        while (fast != null && fast.next != null) {
            slow = slow.next;
            fast = fast.next.next;

            if (slow == fast) {
                return slow;
            }
        }

        return null;
    }
}

Brent 判环算法

Brent 算法跟 Floyd 算法比较起来，其优点是缩短了判断是否有环的耗时（根据 Wikipedia 的说法，Brent 算法的平均耗时比 Floyd 算法少 36%），但是这个算法无法找到环的入口。

这个算法同样会使用快和慢两个指针，判断是否有环的依据仍然是看两个指针是否会相遇，但是快指针和慢指针的走法与 Floyd 算法不同。这个算法中，快指针每一次会向前 2n 步（n 为从 1 开始算起的回合数），即第一回合快指针走 2 步，第二回合走 4 步，以此类推。回合结束后，慢指针直接传送到快指针所在的位置。在每个回合的快指针移动过程中判断快指针是否与慢指针交会，如果交会，那么就判定存在环。

代码：

/**
 * https://leetcode.com/problems/linked-list-cycle
 */
public class Solution {
    public boolean hasCycle(ListNode head) {
        ListNode slow = head;
        ListNode fast = head;

        // 当前回合快指针已走的步数
        int stepsMovedByFast = 0;
        // 当前回合快指针最多能走的步数
        int stepLimitForFast = 2;

        while (fast != null && fast.next != null) {
            fast = fast.next;
            stepsMovedByFast++;

            // 如果快指针往前走的时候与慢指针相会
            // 那就说明链表中存在环
            if (fast == slow) {
                return true;
            }

            // 快指针走完了能走的步数，即回合结束
            if (stepsMovedByFast == stepLimitForFast) {
                // 快指针在下一回合能走的步数翻倍
                stepLimitForFast *= 2;
                // 清零计步器
                stepsMovedByFast = 0;

                // 慢指针传送到快指针所在的位置
                slow = fast;
            }
        }

        return false;
    }
}